고대 사람들의 수(NUMBERS), 구고현 정리(피타고라스 정리)와 원적문제 그리고 파이(원주율)
1. 구고현 정리(피타고라스 정리)

높이 구, 밑변 고, 빗변 현으로 이루어진 구고현정리는 우리가 학교에서 피타고라스 정리라고 배운 그 법칙으로 이는 서양뿐 아니라 중국에서도 가장 기본이 되는 법칙입니다.
사각형은 곡촉으로 풀고 곡촉은 구구단으로 풀어나갑니다.
밑변이 3, 높이가 4인 직각 삼각형이 있습니다.

이 삼각형은 가로가 3이고 세로가 4인 직사각형의 절반입니다.
따라서 그 면적은 3X4=12의 절반인 6입니다.
똑같은 직각 삼각형을 세 개 더 만들어 붙여 위와 같이 정사각형을 만들었습니다.

면적은 6+6+6+6+1=25입니다.

정사각형 한 변의 길이는 5입니다.
따라서 밑변 3, 높이 4인 직각삼각형의 빗변은 5가 되므로 구고현정리(피타고라스 정리)에 대한 증명이 끝났습니다.
그리고 이제부터 구고현 정리 이것을 들고 하늘과 땅을 재러 갑니다.
2. 구고현정리를 통한 주기별 태양이 도는 중심 계산
하늘이 내어주는 작은 기미들을 끈질기게 살피던 이들은 하늘의 움직임을 땅에다 옮겨놓습니다.
기다란 막대기 하나를 땅에 꽂자 모든 것이 풀립니다.
하늘과 땅을 측정할 때는 반드시 구고현의 정리를 써야 했습니다.
구고현에서 이 막대는 직각을 이루어야 하므로 수직으로 꽂혀 있어야만 합니다.

여덟 자의 막대기를 꽂으면 저절로 직각삼각형이 만들어지며, 이것이 구고현의 '구'입니다.
이 막대기를 비추는 해의 그림자는 구고현의 '고'입니다.
그리고 이것에 빗변을 그으면 '현'이 됩니다.
하짓날 정오의 그림자가 1.6자(1cm=0.033자(尺))라고 한다면 이 막대를 하늘로 1만 배 연장시키고 그림자의 끝도 연장시키면 거꾸로 된 직각삼각형이 만들어집니다.

거꾸로 된 직각삼각형의 '구'가 생길 텐데 그 길이는 땅에 있는 '구'의 1만 배입니다.
따라서 그림자가 1.6자이기 때문에 위의 길이는 1만 6천 리가 됩니다.
이 공식을 통해 하짓날 정오 때 태양의 위치를 측정할 수 있습니다.
같은 방식으로 해가 가장 낮게 뜨는 동지 때 태양까지 거래를 재는 것도 가능하며, 춘분과 추분 때도 마찬가지입니다.
이렇게 1년 365일 지구의 그림자를 쟀으며 하지 때 태양의 위치를 알고 역시 주기를 이용해 태양이 도는 중심을 계산합니다.
결국 하지 때 지구중심에서 태양에 이르는 거리가 나왔습니다.
3. 하늘의 수를 알기 위한 사람들의 예와 법도
11만 9천 리(1cm=0.000025리(里)), 태양궤도는 바로 이 원둘레입니다.
어떤 원이라도 지름과 원둘레의 비율은 일정합니다.
거대중국인들에게 그 비율은 3이었습니다.
하지 때 태양궤도는 71만 4천 리, 현대과학과 수치는 다르지만 그것은 측량의 문제이지 원리는 같습니다.
달력을 반포하기 전에는 하늘에 큰 제를 올렸습니다.
하늘의 시간을 인간에게 준다
이것으로 백성들이 씨를 뿌릴 때를 알았고, 조상의 제삿날을 알았습니다.
예와 법도가 섰습니다.
예의식은 그가 완벽한 하늘의 이치를 땅에 실현시키겠다는 맹세입니다.
소의 안이 순결하다는 의미로 소의 피를 하늘에 바쳤고, 소의 겉이 순결하다는 의미로 소의 귀털을 하늘에 바치며 하늘의 수를 알기 위한 사람의 일이 이제 끝나게 됩니다.
4. '자와 컴퍼스'만 가지고 기하학적 건축물을 만드는 것이 그리스식 논리
'아낙사고라스'는 반골의 학자로 하늘은 원이고 땅은 네모라고 생각했습니다.
그리스 아테네의 모든 지성들은 아크로폴리스에 모여 우주와 인간의 문제에 대해 고민을 했습니다.

아테나 여신에게 바쳐 전 '파르테논 신전'은 그리스인들의 논리만큼 견고하고 아름답습니다.
https://donbuller.tistory.com/entry/신들의사생활2-4
신들의 사생활 2-4(그리스 로마 신화/이상한 변호사 아테나와 앙숙 포세이돈, 최초의 피고인 아레
신들의 사생활 2-4(그리스 로마 신화/이상한 변호사 아테나와 앙숙 포세이돈, 최초의 피고인 아레스) 1. 아테나, 케크로피아의 수호신이 되기로 하다 지금으로부터 몇천 년 전일지 헤아릴 수도 없
donbuller.tistory.com
https://donbuller.tistory.com/entry/신들의사생활2-11
신들의 사생활 2-11(그리스 로마 신화/올림포스 3대 미녀 아프로디테, 헤라, 아테나와 목동 파리스
신들의 사생활 2-11(그리스 로마 신화/올림포스 3대 미녀 아프로디테, 헤라, 아테나와 목동 파리스이야기) 1. 테티스 여신과의 사이에서 낳은 자식이 하늘을 다스리게 될 것이라는 예언 때문에 자
donbuller.tistory.com
한치의 오류도 허용하지 않겠다는 듯 단단한 공리 위에 세워져 있습니다.
그리스인의 강박관념을 잘 보여주는 것이 바로 자와 컴퍼스이며, 이것을 사용하는 것이 경제적이며 공리에 있어 효과적이기 때문입니다.
그리스인들은 자와 컴퍼스만 이용해 기하학적 건축물을 만드는 것이 가능했고 다른 흥미로운 건축물도 만들고 싶어 했습니다.
두 점을 이으면 직선이다
이런 자명한 공리 위에 오직 자와 컴퍼스만 가지고 하나씩 차곡차곡 쌓아 올린 것이 바로 그리스식 논리입니다.
수학자라면 기꺼이 들어가 보고 싶은 감옥일 것입니다.
5. 원적문제, 원과 똑같은 면적이 되는 정사각형을 작도하는 것
불경죄로 감옥에 갇혔으면서도 아낙사고라스는 어떤 수학문제를 풀었습니다.
하늘은 원이고 땅은 네모라고 생각하는 사람이 빠질만한 문제이며 이 문제는 나중에 아낙사고라스보다 더 유명해집니다.
바로 '원적문제'인데, 이 원적문제는 고대 기하학에서 아주 유명한 문제입니다.
기하학적 원리에 따라 원과 같은 면적의 정사각형을 자와 컴퍼스로만 그려내는 문제입니다.

원에 내접하는 정사각형이 있습니다.
이 정사각형은 원보다 작습니다.
반대로 원에 외접하는 정사각형이 있습니다.
이 정사각형은 원보다 큽니다.
그 사이 어디엔가 원과 똑같은 면적이 되는 정사각형이 있을 것 같습니다.
이것을 작도하는 것이 '원적문제'입니다.
직선으로 곡선을 알아낸다는 것
으로 이것은 터무니없는 일만은 아닙니다.
키오스의 히포크라테스가 이미 곡선으로 둘러싸인 도형의 넓이를 구한 적이 있었기 때문입니다.

이것을 일명 '히포크라테스의 초승달'이라고 합니다.

피타고라스의 정리에 따라 직각삼각형의 짧은 변 두 개로 만든 정사각형의 면적은 빗변으로 만든 정사각형의 면적과 같습니다.
형태가 어떻게 변해도 위 두 개의 면적은 아래 하나와 같습니다.
따라서 아래 반달은 나머지 두 반달을 더한 면적과 같습니다.
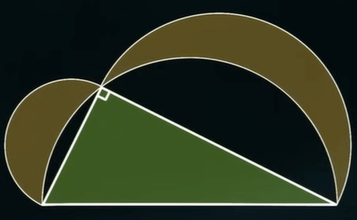
아래 반달을 위로 올려 겹친 부분을 뺍니다.
그렇게 되면 반달의 남은 부분은 크기가 직각삼각형과 같습니다.
원과 같은 정사각형도 할 수 있을 것 같았지만, 이 문제가 2천 년 넘게 안 풀릴 줄은 아무도 몰랐습니다.
6. 아르키메데스, 원의 문제를 직각삼각형의 문제로 바꾸다

1999년 경매장에 책이 한 권 나왔습니다.
고서 복원가 윌리엄 노엘이 그 책을 보았고, 분명 레오나르도 다 빈치 또한 그 책을 봤을 것입니다.
놀라운 것은 이 책이 어떤 책을 베낀 필사본인데 그 밑에 또 다른 글이 숨겨져 있었던 것입니다.
바로 '복기지'였습니다.
이 복기지는 수백 년 동안 숨겨져 왔는데, 기독교인들이 숨겼습니다.
기독교인들이 이 복기지를 숨겼던 이유는 그 내용이 얼마나 중요한지 알았기 때문입니다.
서기 940년, 한 수도승이 자신이 아끼던 책 한 권을 손으로 베꼈습니다.
벌써 이전부터 손에서 손으로 이미 천 년을 내려오고 있는 책이었습니다.
그로부터 300년쯤 지나 한 신부가 이 글자들을 지워버리고, 그 위에 자신이 좋아하는 기도문을 옮겨 적습니다.
고서 수집가가 이 책을 구매한 가격은 22억 원가량입니다.
촛농과 아교가 잔뜩 뭍은 채, 천년만에 나타난 이 책은 학자들이 읽을 수 있게 되기까지 2년이 걸렸습니다.
7~8년 더 복원하는 동안에 점점 더 많은 학자들이 이 책에 관심을 보였으며 이 책은 인류가 오랫동안 찾고 있던 책이었습니다.
기도문이 덮어 버린 고대 그리스의 글자들, 그리고 원이 복원되었고, 이 책을 쓴 사람이 바로 아르키메데스입니다.
아르키메데스는 여기 시칠리아의 시라쿠사에서 태어나 활동했습니다.

이 반사경은 시라쿠사가 로마와 전쟁할 때 만든 것으로 로마 전함을 불태우기 위해 만들어진 아르키메데스의 발명품입니다.


이것은 그가 이집트 유학 중에 만든 나선식 펌프로 낮은 곳에서 물을 끌어올리는 기구로 농사를 지을 때 매우 유용합니다.
그리스 변방의 이 과학자는 자와 컴퍼스로 논리를 따지는 대신, 직접 재고 만들었습니다.
그가 살았던 시대의 시라쿠사는 로망군에게 여러 번 침공을 받았습니다.
작은 시라쿠사가 오래 저항할 수 있었던 것은 그가 만든 무기 덕분이었습니다.
아르키메데스는 한 시대는 더 일찍 태어난 사람으로 칭송받고 있는 인물로, 고대에서 가장 위대한 물리학자이자 수학자 중 하나로 손꼽히고 있습니다.
그는 '파이란 무엇인가'와 같은 수학에도 큰 관심을 가지고 있었습니다.
아낙사고라스가 처음 문제를 낸 이후 원적문제는 여전히 인기가 좋았는데, 아르키메데스는 좀 다른 방식으로 문제에 접근합니다.
그는 원 면적을 구하는 일에 집중했는데, 그리스 중심에서 멀리 떨어져 있었던 탓인지 그에게는 자와 컴퍼스에 대한 강박이 없었습니다.
아르키메데스의 방식은 이러했습니다.

먼저 원을 네 조각냅니다.

그것을 펼치는 이런 모양입니다.

그와 똑같은 모양을 위에 끼여 맞추는데 이것은 원 두 개를 위아래로 붙인 셈이 됩니다.

이 원을 더 잘게, 더 잘게, 더 잘게 조각냅니다.

점점 아래의 곡선은 직선이 되고 마침내 직사각형이 될 것입니다.

직사각형의 절반인 직각삼각형은 원면적과 같고, 원둘레는 직각삼격형의 밑변입니다.
그런데 이 길이를 잴 수가 없습니다.
원의 문제를 직각삼각형의 문제로 바꾼 것은 획기적인 아이디어였지만, 그래도 길이는 알 수 없었습니다.
7. 원주율(파이)을 그리는 방법
세상에 수많은 크기의 원이 있습니다.
우리가 이 원에 대해 아는 것은 반지름이 커지면 원도 커진다는 것입니다.
그런데 그 비율이 얼마인지는 정확히 모릅니다.
그렇다면 원이란 도대체 무엇일까요?
아르키메데스는 정말 똑똑했습니다.
그리스인들은 다양한 다각형의 넓이와 둘레를 구하는 방법을 알았습니다.
그래서 아르키메데스는 원보다 작은 다각형과 원보다 큰 다각형 사이에 원을 집어넣었습니다.

원에 내접하는 육각형의 지름이 1이라면 육각형의 둘레는 3입니다.
원에 외접하는 육각형의 지름이 1이라면 육각형의 둘레는 3.4641입니다.
두 두 숫자 사이에 원둘레가 있습니다.
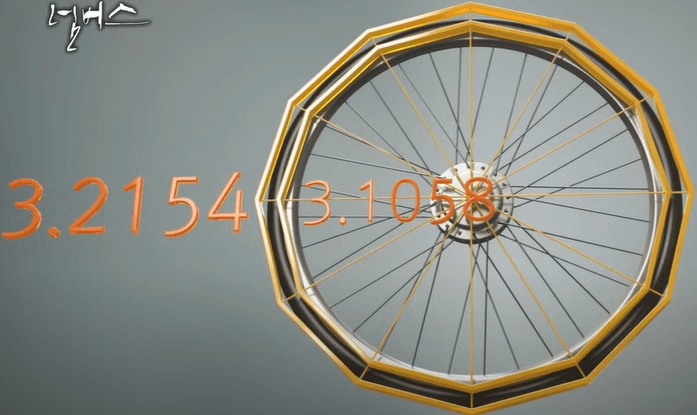
다음으로 내접하는 육각형을 쪼개 12 각형을 그려 나온 둘레는 3.1058입니다.
외접하는 육각형도 쪼개 12 각형을 그려 나온 둘레는 3.2154입니다.
이런 식으로 계속해서 다각형을 더 잘게 쪼갤수록 두 숫자의 간격은 좁아져서 점점 파이값에 다가가게 됩니다.
이것을 무한히 계산할 수 있다면 즉, 면의 수를 무한히 늘릴 수 있다면 파이 값을 구할지도 모릅니다.
아르키메데스는 막대기를 들고 논리로 무장하고 우리는 원을 향해 걸어왔습니다.
그는 가는 법은 알지만 길이 없었고, 못 가는 줄 알면서도 계속 걸었습니다.
인생에서 하루가 남았다면 혹은 한 시간이 남았다면 무엇을 하게 될까요?
아르키메데스는 죽는 순간까지 '원'을 잡고 있었던 것으로 보입니다.

1965년 아르키메데스의 무덤이 발견되었는데, 그 진위여부를 두고 말이 많았습니다.
죽은 지 2천 년이 넘었는데 아르키메데스는 그 이름 하나만으로도 여전히 이슈가 됩니다.
그가 그린 원은 어떻게 됐을까요?
후대 사람들은 계속해서 아르키메데스의 방식대로 파이값을 구했습니다.
360 각형 3.14166, 3072 각형 3.1416, 24576 각형 3.141592, 805306368 각형 3.14159265358979324, 32212254720 각형 3.1415926535897932384
1882년 이 행렬은 멈추게 됩니다.
파이는 방정식의 답도 될 수 없고 무한하게 계속되는 수라는 것이 밝혀진 것입니다.
원적문제는 풀 수 없는 불가능의 문제였으며 인간의 힘으로는 결코 닿을 수 없는 존재가 바로 '파이'입니다.
https://donbuller.tistory.com/entry/소수
소수를 찾기 위한 천재 수학자들의 도전
소수를 찾기 위한 천재 수학자들의 도전1. 소수란? 소수는 아주 특별한 성질을 가진 숫자입니다.소수는 1과 자신을 제외하면 어떤 수로도 나눠지지 않는 수를 말합니다.이 소수에는 많은 수
donbuller.tistory.com
<출처:EBS지식>
'돈벌러와 함께하는 생활의 팁' 카테고리의 다른 글
| 한번 녹았다 다시 얼린 아이스크림은 왜 맛이 없을까요? (0) | 2024.08.09 |
|---|---|
| 문해력, 독해력, 지능, 사고력을 기르는 자녀 교육 방법 (0) | 2024.07.17 |
| 소수를 찾기 위한 천재 수학자들의 도전 (0) | 2024.07.12 |
| 초고령자가 고집스럽게 똑같은 일을 하는 이유 (0) | 2024.07.11 |
| 콜레라, 영국의 제국주의가 확산시켜 일곱 번의 팬데믹을 일으킨 감염병 (0) | 2024.07.05 |



